Variational autoencoders

$\newcommand{\D}{\mathcal{D}} \newcommand{\KL}[2]{D_\mathrm{KL}\paren{#1 \mathbin{\|} #2}} \newcommand{\P}{\mathcal{P}} \newcommand{\X}{\mathcal{X}} \newcommand{\Z}{\mathcal{Z}} \newcommand{\Q}{\mathcal{Q}} \newcommand{\bx}{\mathbf{x}} \newcommand{\M}{\mathcal{B}} \newcommand{\ELBO}{\mathrm{ELBO}} \newcommand{\bz}{\mathbf{z}} \newcommand{\giv}{\mid} \newcommand{\paren}[1]{\left(#1\right)} \newcommand{\brac}[1]{\left[#1\right]} \newcommand{\veps}{\varepsilon} \newcommand{\set}[1]{\left\{#1\right\}} \renewcommand{\d}{\mathop{}\!\mathrm{d}} \newcommand{\Expect}{\mathbb{E}} \newcommand{\Normal}{\mathcal{N}} \newcommand{\I}{\mathbf{I}} \newcommand{\0}{\mathbf{0}} \DeclareMathOperator*{\argmin}{arg\,min} \DeclareMathOperator*{\argmax}{arg\,max}$

Latent variable models form a rich class of probabilistic models that can infer hidden structure in the underlying data. In this post, we will study variational autoencoders, which are a powerful class of deep generative models with latent variables.

Representation

Consider a directed, latent variable model as shown below.

drawing — Graphical model for a directed, latent variable model.

In the model above, $\bz$ and $\bx$ denote the latent and observed variables respectively. The joint distribution expressed by this model is given as

$p_\theta(\bx, \bz) = p(\bx \giv \bz)p(\bz).$

From a generative modeling perspective, this model describes a generative process for the observed data $\bx$ using the following procedure

$\begin{align} \bz &\sim p(\bz) \\ \bx &\sim p(\bx \giv \bz). \end{align}$

If one adopts the belief that the latent variables $\bz$ somehow encode semantically meaningful information about $\bx$ , it is natural to view this generative process as first generating the “high-level” semantic information about $\bx$ first before fully generating $\bx$ . Such a perspective motivates generative models with rich latent variable structures such as hierarchical generative models $p(\bx, \bz_1, \ldots, \bz_m) = p(\bx \giv \bz_1)\prod_i p(\bz_i \giv \bz_{i+1})$ —where information about $\bx$ is generated hierarchically—and temporal models such as the Hidden Markov Model—where temporally-related high-level information is generated first before constructing $\bx$ .

We now consider a family of distributions $\P_\bz$ where $p(\bz) \in \P_\bz$ describes a probability distribution over $\bz$ . Next, consider a family of conditional distributions $\P_{\bx\giv \bz}$ where $p_\theta(\bx \giv \bz) \in \P_{\bx\giv \bz}$ describes a conditional probability distribution over $\bx$ given $\bz$ . Then our hypothesis class of generative models is the set of all possible combinations

$\begin{align} \P_{\bx,\bz} = \set{p(\bx, \bz) \giv p(\bz) \in \P_\bz, p(\bx \giv \bz) \in \P_{\bx\giv\bz}}. \end{align}$

Given a dataset $\D = \set{\bx^{(1)}, \ldots, \bx^{(n)}}$ , we are interested in the following learning and inference tasks

Selecting $p \in \P_{\bx,\bz}$ that “best” fits $\D$ .
Given a sample $\bx$ and a model $p \in \P_{\bx,\bz}$ , what is the posterior distribution over the latent variables $\bz$ ?

Learning Directed Latent Variable Models

One way to measure how closely $p(\bx, \bz)$ fits the observed dataset $\D$ is to measure the Kullback-Leibler (KL) divergence between the data distribution (which we denote as $p_{\mathrm{data}}(\bx)$ ) and the model’s marginal distribution $p(\bx) = \int p(\bx, \bz) \d \bz$ . The distribution that ``best’’ fits the data is thus obtained by minimizing the KL divergence.

$\begin{align} \min_{p \in \P_{\bx, \bz}}\KL{p_{\mathrm{data}}(\bx)}{p(\bx)}. \end{align}$

As we have seen previously, optimizing an empirical estimate of the KL divergence is equivalent to maximizing the marginal log-likelihood $\log p(\bx)$ over $\D$

$\begin{align} \max_{p \in \P_{\bx, \bz}} \sum_{\bx \in \D} \log p(\bx) = \sum_{\bx \in \D} \log\int p(\bx, \bz) \d \bz. \end{align}$

However, it turns out this problem is generally intractable for high-dimensional $\bz$ as it involves an integration (or sums in the case $\bz$ is discrete) over all the possible latent sources of variation $\bz$ . One option is to estimate the objective via Monte Carlo. For any given datapoint $\bf x$ , we can obtain the following estimate for its marginal log-likelihood

$\log p(\bx) \approx \log \frac{1}{k} \sum_{i=1}^k p(\bx \vert \bz^{(i)}) \text{, where } \bz^{(i)} \sim p(\bz)$

In practice however, optimizing the above estimate suffers from high variance in gradient estimates.

Rather than maximizing the log-likelihood directly, an alternate is to instead construct a lower bound that is more amenable to optimization. To do so, we note that evaluating the marginal likelihood $p(\bx)$ is at least as difficult as as evaluating the posterior $p(\bz \mid \bx)$ for any latent vector $\bz$ since by definition $p(\bz \mid \bx) = p(\bx, \bz) / p(\bx)$ .

Next, we introduce a variational family $\Q$ of distributions that approximate the true, but intractable posterior $p(\bz \mid \bx)$ . Further henceforth, we will assume a parameteric setting where any distribution in the model family $\P_{\bx, \bz}$ is specified via a set of parameters $\theta \in \Theta$ and distributions in the variational family $\Q$ are specified via a set of parameters $\lambda \in \Lambda$ .

Given $\P_{\bx, \bz}$ and $\Q$ , we note that the following relationships hold true¹ for any $\bx$ and all variational distributions $q_\lambda(\bz) \in \Q$

$\begin{align} \log p_\theta(\bx) &= \log \int p_\theta(\bx, \bz) \d \bz \\ &= \log \int \frac{q_\lambda(\bz)}{q_\lambda(\bz)} p(\bx, \bz) \d \bz\\ &\ge\int q_\lambda(\bz) \log \frac{p_\theta(\bx, \bz)}{q_\lambda(\bz)} \d \bz \\ &= \Expect_{q_\lambda(\bz)} \left[\log \frac{p_\theta(\bx, \bz)}{q_\lambda(\bz)}\right] \\ &:=\ELBO(\bx; \theta, \lambda) \end{align}$

where we have used Jensen’s inequality in the final step. The Evidence Lower Bound or ELBO in short admits a tractable unbiased Monte Carlo estimator

$\begin{align} \frac{1}{k} \sum_{i=1}^k \log \frac{p_\theta(\bx, \bz^{(i)})}{q_\lambda(\bz^{(i)})} \text{, where } \bz^{(i)} \sim q_\lambda(\bz), \end{align}$

so long as it is easy to sample from and evaluate densities for $q_\lambda(\bz)$ .

Which variational distribution should we pick? Even though the above derivation holds for any choice of variational parameters $\lambda$ , the tightness of the lower bound depends on the specific choice of $q$ .

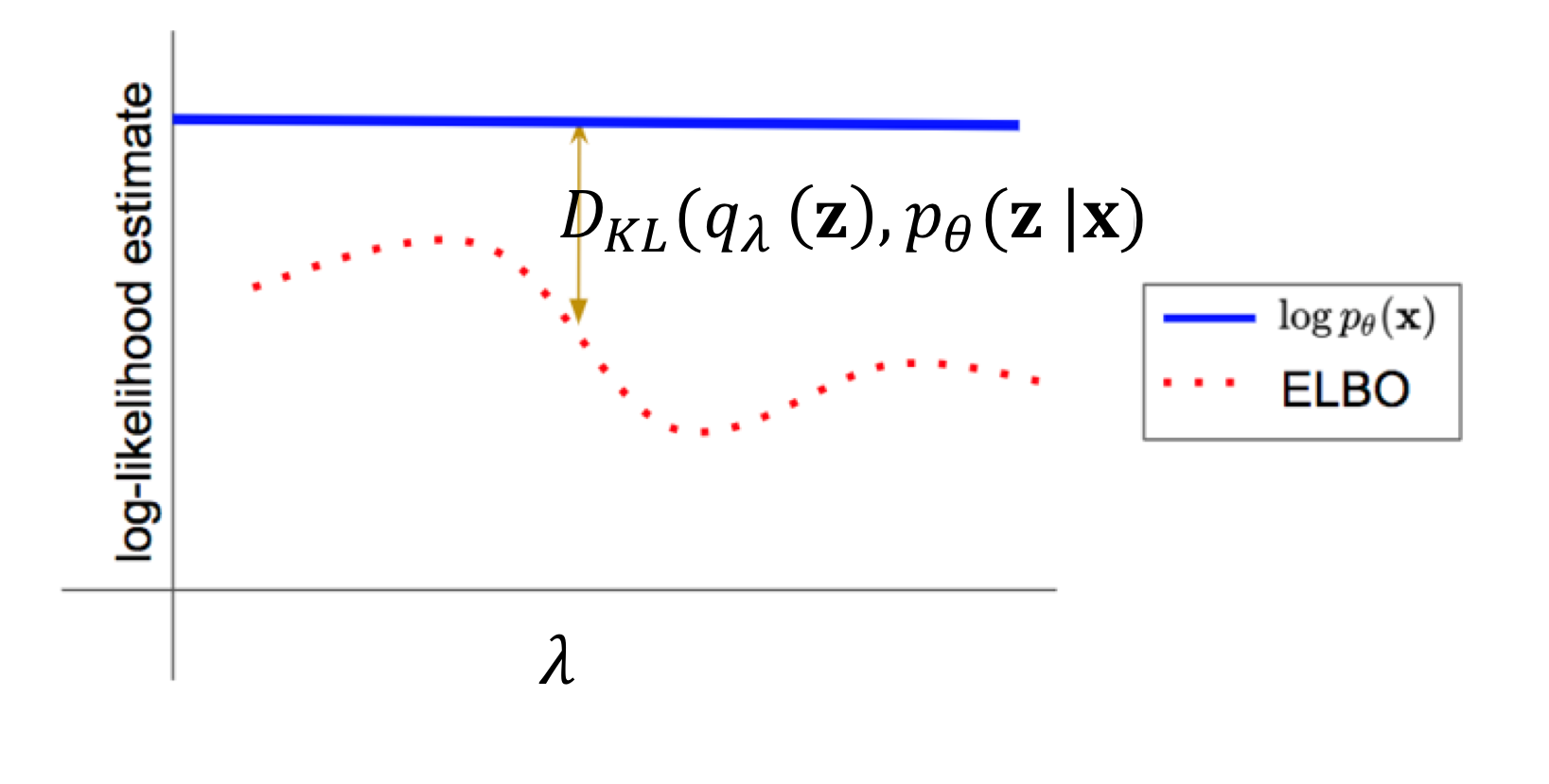
In particular, the gap between the original objective(marginal log-likelihood $\log p_\theta(\bx)$ ) and the ELBO equals the KL divergence between the approximate posterior $q(\bz)$ and the true posterior $p(\bz \giv \bx)$ . The gap is zero when the variational distribution $q_\lambda(\bz)$ exactly matches $p_\theta(\bz \giv \bx)$ .

In summary, we can learn a latent variable model by maximizing the ELBO with respect to both the model parameters $\theta$ and the variational parameters $\lambda$ for any given datapoint $\bx$

$\begin{align} \max_{\theta} \sum_{\bx \in \D} \max_{\lambda} \Expect_{q_\lambda(\bz)} \left[\log \frac{p_\theta(\bx, \bz)}{q_\lambda(\bz)}\right]. \end{align}$

Black-Box Variational Inference

In this post, we shall focus on first-order stochastic gradient methods for optimizing the ELBO. These optimization techniques are desirable in that they allow us to sub-sample the dataset during optimization—but require our objective function to be differentiable with respect to the optimization variables. This inspires Black-Box Variational Inference (BBVI), a general-purpose Expectation-Maximization-like algorithm for variational learning of latent variable models, where, for each mini-batch $\M = \set{\bx^{(1)}, \ldots, \bx^{(m)}}$ , the following two steps are performed.

Step 1

We first do per-sample optimization of $q$ by iteratively applying the update

$\begin{align} \lambda^{(i)} \gets \lambda^{(i)} + \tilde{\nabla}_\lambda \ELBO(\bx^{(i)}; \theta, \lambda^{(i)}), \end{align}$

where $\text{ELBO}(\bx; \theta, \lambda) = \Expect_{q_\lambda(\bz)} \left[\log \frac{p_\theta(\bx, \bz)}{q_\lambda(\bz)}\right]$ , and $\tilde{\nabla}_\lambda$ denotes an unbiased estimate of the ELBO gradient. This step seeks to approximate the log-likelihood $\log p_\theta(\bx^{(i)})$ .

Step 2

We then perform a single update step based on the mini-batch

$\begin{align} \theta \gets \theta + \tilde{\nabla}_\theta \sum_{i} \ELBO(\bx^{(i)}; \theta, \lambda^{(i)}), \end{align}$

which corresponds to the step that hopefully moves $p_\theta$ closer to $p_{\mathrm{data}}$ .

Gradient Estimation

The gradients $\nabla_\lambda \ELBO$ and $\nabla_\theta \ELBO$ can be estimated via Monte Carlo sampling. While it is straightforward to construct an unbiased estimate of $\nabla_\theta \ELBO$ by simply pushing $\nabla_\theta$ through the expectation operator, the same cannot be said for $\nabla_\lambda$ . Instead, we see that

$\begin{align} \nabla_\lambda \Expect_{q_\lambda(\bz)} \left[\log \frac{p_\theta(\bx, \bz)}{q_\lambda(\bz)} \right]= \Expect_{q_\lambda(\bz)} \brac{\paren{\log \frac{p_\theta(\bx, \bz)}{q_\lambda(\bz)}} \cdot \nabla_\lambda \log q_\lambda(\bz)}. \end{align}$

This equality follows from the log-derivative trick (also commonly referred to as the REINFORCE trick). The full derivation involves some simple algebraic manipulations and is left as an exercise for the reader. The gradient estimator $\tilde{\nabla}_\lambda \ELBO$ is thus

$\begin{align} \frac{1}{k}\sum_{i=1}^k \brac{\paren{\log \frac{p_\theta(\bx, \bz^{(i)})}{q_\lambda(\bz^{(i)})}} \cdot \nabla_\lambda \log q_\lambda(\bz^{(i)})} \text{, where } \bz^{(i)} \sim q_\lambda(\bz). \end{align}$

However, it is often noted that this estimator suffers from high variance. One of the key contributions of the variational autoencoder paper is the reparameterization trick, which introduces a fixed, auxiliary distribution $p(\veps)$ and a differentiable function $T(\veps; \lambda)$ such that the procedure

$\begin{align} \veps &\sim p(\veps)\\ \bz &\gets T(\veps; \lambda), \end{align}$

is equivalent to sampling from $q_\lambda(\bz)$ . By the Law of the Unconscious Statistician, we can see that

$\begin{align} \nabla_\lambda \Expect_{q_\lambda(\bz)} \left[\log \frac{p_\theta(\bx, \bz)}{q_\lambda(\bz)}\right] = \Expect_{p(\veps)} \left[\nabla_\lambda \log \frac{p_\theta(\bx, T(\veps; \lambda))}{q_\lambda(T(\veps; \lambda))}\right]. \end{align}$

In contrast to the REINFORCE trick, the reparameterization trick is often noted empirically to have lower variance and thus results in more stable training.

Parameterizing Distributions via Deep Neural Networks

So far, we have described $p_\theta(\bx, \bz)$ and $q_\lambda(\bz)$ in the abstract. To instantiate these objects, we consider choices of parametric distributions for $p_\theta(\bz)$ , $p_\theta(\bx \giv \bz)$ , and $q_\lambda(\bz)$ . A popular choice for $p_\theta(\bz)$ is the unit Gaussian

$\begin{align} p_\theta(\bz) = \Normal(\bz \giv \0, \I). \end{align}$

in which case $\theta$ is simply the empty set since the prior is a fixed distribution. Another alternative often used in practice is a mixture of Gaussians with trainable mean and covariance parameters.

The conditional distribution $p_\theta(\bx \giv \bz)$ is where we introduce a deep neural network. We note that a conditional distribution can be constructed by defining a distribution family (parameterized by $\omega \in \Omega$ ) in the target space $\bx$ (i.e. $p_\omega(\bx)$ defines an unconditional distribution over $\bx$ ) and a mapping function $g_\theta: \Z \to \Omega$ . In other words, $g_\theta(\cdot)$ defines the conditional distribution

$\begin{align} p_\theta(\bx \giv \bz) = p_\omega(\bx) \text{ , where } \omega = g_\theta(\bz). \end{align}$

The function $g_\theta$ is also referred to as the decoding distribution since it maps a latent code $\bz$ to the parameters of a distribution over observed variables $\bx$ . In practice, it is typical to specify $g_\theta$ as a deep neural network.
In the case where $p_\theta(\bx \giv \bz)$ is a Gaussian distribution, we can thus represent it as

$\begin{align} p_\theta(\bx \giv \bz) = \Normal(\bx \giv \mu_\theta(\bz), \Sigma_\theta(\bz)), \end{align}$

where $\mu_\theta(\bz)$ and $\Sigma_\theta(\bz)$ are neural networks that specify the mean and covariance matrix for the Gaussian distribution over $\bx$ when conditioned on $\bz$ .

Finally, the variational family for the proposal distribution $q_\lambda(\bz)$ needs to be chosen judiciously so that the reparameterization trick is possible. Many continuous distributions in the location-scale family can be reparameterized. In practice, a popular choice is again the Gaussian distribution, where

$\begin{align} \lambda &= (\mu, \Sigma) \\ q_\lambda(\bz) &= \Normal(\bz \giv \mu, \Sigma)\\ p(\veps) &= \Normal(\bz \giv \0, \I) \\ T(\veps; \lambda) &= \mu + \Sigma^{1/2}\veps, \end{align}$

where $\Sigma^{1/2}$ is the Cholesky decomposition of $\Sigma$ . For simplicity, practitioners often restrict $\Sigma$ to be a diagonal matrix (which restricts the distribution family to that of factorized Gaussians).

Amortized Variational Inference

A noticable limitation of black-box variational inference is that Step 1 executes an optimization subroutine that is computationally expensive. Recall that the goal of the Step 1 is to find

$\begin{align} \lambda^* = \argmax_{\lambda\in \Lambda} \ELBO(\bx; \theta, \lambda). \end{align}$

For a given choice of $\theta$ , there is a well-defined mapping from $\bx \mapsto \lambda^\ast$ . A key realization is that this mapping can be learned. In particular, one can train an encoding function (parameterized by $\phi$ ) $f_\phi: \X \to \Lambda$ (where $\Lambda$ is the space of $\lambda$ parameters) on the following objective

$\begin{align} \max_{\phi } \sum_{\bx \in \D} \ELBO(\bx; \theta, f_\phi(\bx)). \end{align}$

It is worth noting at this point that $f_\phi(\bx)$ can be interpreted as defining the conditional distribution $q_\phi(\bz \giv \bx)$ . With a slight abuse of notation, we define

$\begin{align} \ELBO(\bx; \theta, \phi) = \Expect_{q_\phi(\bz \mid \bx)} \left[\log \frac{p_\theta(\bx, \bz)}{q_\phi(\bz \giv \bx)}\right]. \end{align}$

and rewrite the optimization problem as

$\begin{align} \max_{\phi } \sum_{\bx \in \D} \ELBO(\bx; \theta, \phi). \end{align}$

It is also worth noting that optimizing $\phi$ over the entire dataset as a subroutine everytime we sample a new mini-batch is clearly not reasonable. However, if we believe that $f_\phi$ is capable of quickly adapting to a close-enough approximation of $\lambda^\ast$ given the current choice of $\theta$ , then we can interleave the optimization $\phi$ and $\theta$ . The yields the following procedure, where for each mini-batch $\M = \set{\bx^{(1)}, \ldots, \bx^{(m)}}$ , we perform the following two updates jointly

$\begin{align} \phi &\gets \phi + \tilde{\nabla}_\phi \sum_{\bx \in \M} \ELBO(\bx; \theta, \phi) \\ \theta &\gets \theta + \tilde{\nabla}_\theta \sum_{\bx \in \M} \ELBO(\bx; \theta, \phi), \end{align}$

rather than running BBVI’s Step 1 as a subroutine. By leveraging the learnability of $\bx \mapsto \lambda^\ast$ , this optimization procedure amortizes the cost of variational inference. If one further chooses to define $f_\phi$ as a neural network, the result is the variational autoencoder.

Footnotes

The first equality only holds if the support of $q$ includes that of $p$ . If not, it is an inequality. ↩