Introduction

Intelligent agents are constantly generating, acquiring, and processing data. This data could be in the form of images that we capture on our phones, text messages we share with our friends, graphs that model interactions on social media, videos that record important events, etc. Natural agents excel at discovering patterns, extracting knowledge, and performing complex reasoning based on the data they observe. How can we build artificial learning systems to do the same?

In this course, we will study generative models that view the world under the lens of probability. In such a worldview, we can think of any kind of observed data, say $\mathcal{D}$, as a finite set of samples from an underlying distribution, say $p_{\mathrm{data}}$. At its very core, the goal of any generative model is then to approximate this data distribution given access to the dataset $\mathcal{D}$. The hope is that if we are able to learn a good generative model, we can use the learned model for downstream inference.

Learning

We will be primarily interested in parametric approximations to the data distribution, which summarize all the information about the dataset $\mathcal{D}$ in a finite set of parameters. In contrast with non-parametric models, parametric models scale more efficiently with large datasets but are limited in the family of distributions they can represent.

In the parametric setting, we can think of the task of learning a generative model as picking the parameters within a family of model distributions that minimizes some notion of distance¹ between the model distribution and the data distribution.

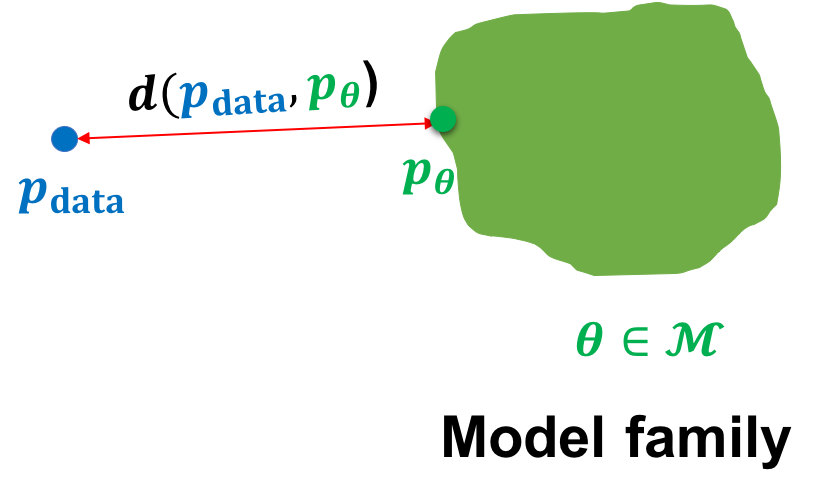
For instance, we might be given access to a dataset of dog images $\mathcal{D}$ and our goal is to learn the paraemeters of a generative model $\theta$ within a model family $\mathcal{M}$ such that the model distribution $p_\theta$ is close to the data distribution over dogs $p_{\mathrm{data}}$. Mathematically, we can specify our goal as the following optimization problem: \begin{equation} \min_{\theta\in \mathcal{M}}d(p_{\mathrm{data}}, p_{\theta}) \label{eq:learning_gm} \tag{1} \end{equation}where $p_{\mathrm{data}}$ is accessed via the dataset $\mathcal{D}$ and $d(\cdot)$ is a notion of distance between probability distributions.

As we navigate through this course, it is interesting to take note of the difficulty of the problem at hand. A typical image from a modern phone camera has a resolution of approximately $700 \times 1400$ pixels. Each pixel has three channels: R(ed), G(reen) and B(lue) and each channel can take a value between 0 to 255. Hence, the number of possible images is given by $256^{700 \times 1400 \times 3}\approx 10 ^{800000}$. In contrast, Imagenet, one of the largest publicly available datasets, consists of only about 15 million images. Hence, learning a generative model with such a limited dataset is a highly underdetermined problem.

Fortunately, the real world is highly structured and automatically discovering the underlying structure is key to learning generative models. For example, we can hope to learn some basic artifacts about dogs even with just a few images: two eyes, two ears, fur etc. Instead of incorporating this prior knowledge explicitly, we will hope the model learns the underlying structure directly from data. There is no free lunch however, and indeed successful learning of generative models will involve instantiating the optimization problem in $(\ref{eq:learning_gm})$ in a suitable way. In this course, we will be primarily interested in the following questions:

• What is the representation for the model family $\mathcal{M}$?
• What is the objective function $d(\cdot)$?
• What is the optimization procedure for minimizing $d(\cdot)$?

In the next few set of lectures, we will take a deeper dive into certain families of generative models. For each model family, we will note how the representation is closely tied with the choice of learning objective and the optimization procedure.

Inference

For a discriminative model such as logistic regression, the fundamental inference task is to predict a label for any given datapoint. Generative models, on the other hand, learn a joint distribution over the entire data.²

While the range of applications to which generative models have been used continue to grow, we can identify three fundamental inference queries for evaluating a generative model.:

1. Density estimation: Given a datapoint $\mathbf{x}$, what is the probability assigned by the model, i.e., $p_\theta(\mathbf{x})$?

2. Sampling: How can we generate novel data from the model distribution, i.e., $\mathbf{x}_{\mathrm{new}} \sim p_\theta(\mathbf{x})$?

3. Unsupervised representation learning: How can we learn meaningful feature representations for a datapoint $\mathbf{x}$?

Going back to our example of learning a generative model over dog images, we can intuitively expect a good generative model to work as follows. For density estimation, we expect $p_\theta(\mathbf{x})$ to be high for dog images and low otherwise. Alluding to the name generative model, sampling involves generating novel images of dogs beyond the ones we observe in our dataset. Finally, representation learning can help discover high-level structure in the data such as the breed of dogs.

In light of the above inference tasks, we note two caveats. First, quantitative evaluation of generative models on these tasks is itself non-trivial (in particular, sampling and representation learning) and an area of active research. Some quantitative metrics exist, but these metrics often fail to reflect desirable qualitative attributes in the generated samples and the learned representations. Secondly, not all model families permit efficient and accurate inference on all these tasks. Indeed, the trade-offs in the inference capabilities of the current generative models have led to the development of very diverse approaches as we shall see in this course.

Footnotes